최단 경로

최단경로 문제

최단경로 문제란 두 노드를 잇는 가장 짧은 경로를 찾는 문제다. 가중치가 있는 그래프(Weighted graph)에서는 가중치의 합이 최소가 되는 경로를 찾는것이 목적이다.

최단경로 문제에는 아래와 같은 변종들이 존재한다.

  • 단일 출발(single-source) 최단경로 :
    • 단일 노드 $v$에서 출발하여 그래프 내 다른 모든 노드에 도착하는 가장 짧은 경로를 찾는 문제
  • 단일 도착(single-destination) 최단 경로 :
    • 모든 노드로부터 출발하여 그래프 내 노드 $v$에 도착하는 가장 짧은 경로를 찾는 문제
  • 단일 쌍(single-pair) 최단 경로 :
    • 주어진 꼭지점 $u$와 $v$에 대해 $u$에서 $v$까지의 최단 경로를 찾는 문제
  • 전체 쌍(all-pair) 최단 경로 :
    • 그래프 내 모든 쌍들 사이의 최단 경로를 찾는 문제

다익스트라 알고리즘, 벨만-포드 알고리즘은 여기서 단일 출발(single-source)최단 경로 문제를 해결하는데 적합하다. 하지만 여기서 조금 더 응용하면 나머지 문제들을 모두 해결 할 수 있다.

optimal substructure

최적 하위구조 : 전체 문제의 답이 부분 문제의 답으로부터 만들어지는 구조 - 주로 동적계획법에서 많이 활용된다.

여기서 최단 경로 문제의 가장 중요한 속성을 하나 짚고 넘어가자.

다익스트라 알고리즘, 벨만-포드 알고리즘이 최단 경로를 구할 때 사용하는 핵심 정리이기도 하다.

최단 경로의 부분 경로는 마찬가지로 최단 경로이다.

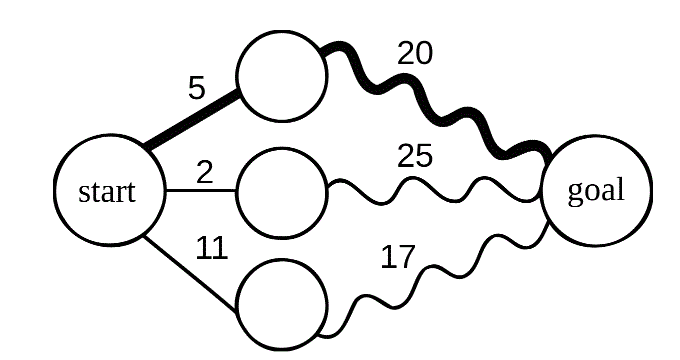
이를 그림으로 나타내면 아래와 같이 표현 가능하다.

edge의 가중치 합이 최소인 최단경로는 굵게 표시된 상단 첫 번째 경로임을 알 수 있다.

그렇다면 start 노드로부터 중간 노드(가중치가 5) 또한 최단 경로라는 것이 핵심 정리다.

이 핵심 정리에 대한 증명은 아래와 같다.

($Puv > P’uv$ 일 때 $w(P)$가 최단경로라는 가정에 대한 모순을 증명)

위 정리를 확장하면 최단경로를 다음과 같이 분해할 수 있다.

시작 노드 $s$에서 $v$에 이르는 최단경로($s$ ~ $v$)는 ($s$ ~ $u$) + ($u$ ~ $v$)다.

식 : $D(s, v) = D(s, u) + w(u, v)$

만약 위 식의 우변의 값 ($D(s, u) + w(u, v)$, 현재 step에서 구한 새로운 경로의 거리)이 좌변($D(s, v)$, 기존 최단경로의 거리)보다 작다면 최단경로를 업데이트해준다.

이렇게 노드별로 하나씩 경로를 구해 확장해나가면 $s$에서 $v$ 사이의 최단 경로를 구할 수 있다.

이와같이 어떤 문제의 최적해가 부분문제들의 최적해들로 구성(construct)될 수 있다면 해당 문제는 optimal structure를 가진다고 말한다.

edge relaxation

최단 경로를 구하는 알고리즘은 **edge relaxation(엣지 경감)**을 기본 연산으로 한다.

이는 지금까지 이야기한 최단경로 문제의 optimal structure에서 파생된 것이다.

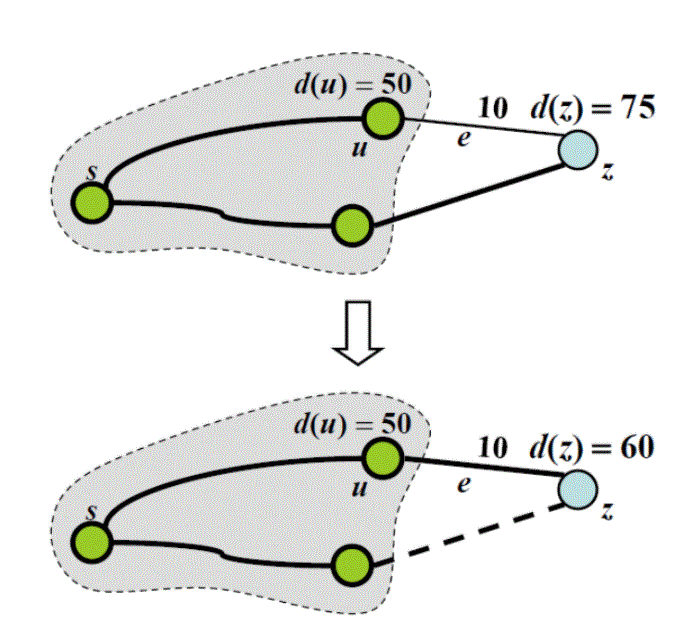
우선 시작 노드 $s$에서 임의의 노드 $z$로의 최단 경로를 구한다고 하자.

  • 현재 알고 있는 $s, z$사이의 최단 경로 $d(z)$는 75
  • 현재 알고 있는 $s, u$사이의 최단 경로 $d(u)$는 50

그런데 탐색 과정에서 엣지 $e$를 경유하여 $z$로 가는 경로의 길이가 총 60이라 한다면 기존에 알고있는 $d(z) = 75$보다 짧기 때문에 기존의 $d(z)$가 최단 경로라고 할 수 없다. 따라서 최단 경로를 구성하고 있는 노드와 엣지의 정보, 그리고 거리의 합을 업데이트 한다. 이게 바로 edge relaxation이다.

인용 : edge relaxation은 최단경로 알고리즘을 수행하는 과정에서 경로를 구성하고 있는 엣지 가중치의 합을 줄여나간다(relax)는 취지로 이런 이름이 붙은 것 같습니다.

참고 자료