벨만 포드 알고리즘

참고 자료

키워드

  • Memozation
  • Graph
  • 최단거리
  • $O(N^3)$

개념

벨만-포드 알고리즘은 $s$, $u$ 사이의 최단 경로를 구할 때 경로의 길이(최대 $V-1$)만큼 전체 edge($E$)를 edge relaxation을 해야 한다.

  • $s$를 제외한 모든 노드의 수($V-1$)만큼 하는 이유
    • 최악의 경우가 V-1인 경우임.
    • 사실상 각 경로 비교에서 최단거리가 갱신된 노드들만 검사해도 무방(최적화)
    • 경로는 순환을 포함해서는 안되므로 경로의 최대 길이(갯수아님)는 V-1
      • 루프 V-1 중 k번째 연산은 $s$로 부터 각 노드까지 k 길이의 간선을 거쳐서 도달할 수 있는 최단 경로를 갱신
      • 기억! 벨만 포드에서의 V-1은 노드 사이의 길이
    • 각 노드를 지나는 경로에 대한 가중치 계산 및 업데이트(이건 내가 푼 방식임)
      • (같은 노드를 두 번 지나지 않는 경우) 각 노드를 지나는 최대 경로는 V-1
  • $O(N-1) * O(E) = O(N * N^2) = O(N^3)$

예시를 통한 설명

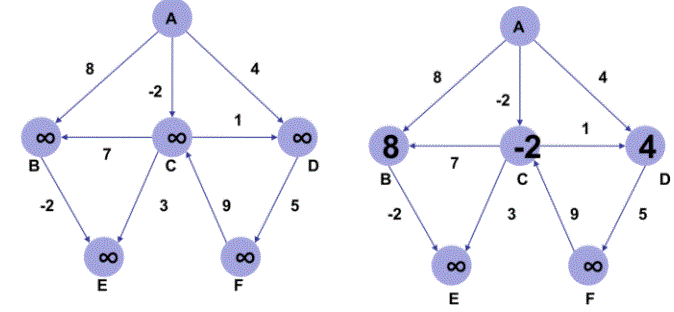
위 그림에서 A로부터 시작하는 다른 노드까지의 최단거리를 구한다고 가정하자

한 번 edge relaxation을 할 때 마다 k개 간선을 이용해서 이동 가능한 거리의 가중치와의 비교를 뜻한다고 하였다.

위 그림에서 한 개 간선을 이용해서 이동 가능한 edge relaxation을 수행한다면 B, C, D가 갱신될 것이다.

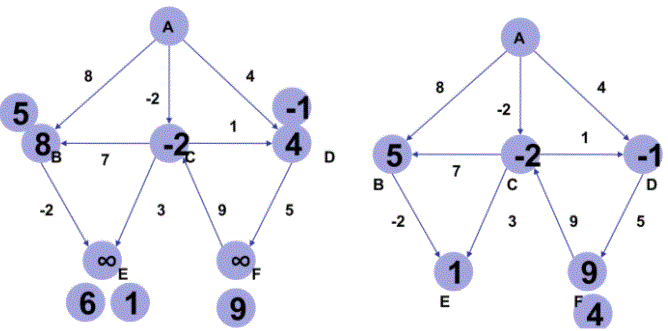
그리고 다시 위 그림의 좌측은 두 개 간선을 이용했을 때 갱신 여부, 우측은 세 개 간선을 이용했을때 갱신 여부다.

물론 가중치 갱신은 이 전의((k-1번째 까지 계산된) 최단거리와 비교하여 현재(k번째까지 계산)가 더 단거리라면 갱신하고 그렇지 않다면 그대로 유지한다.

이러한 방식으로 벨만 포드알고리즘은 모든 간선에 대해서 edge relaxation을 최대 V-1번 수행함으로써 start부터 각 노드까지의 최단거리를 구한다.

다익스트라 알고리즘과 함께 그래프의 최단거리를 구할 때 많이 사용된다. 다만 다익스트라와 다르게 edge 계산 대상 노드를 선택하는 과정에서 우선순위(가중치 등)를 고려하지 않고 모든 노드에 대해서 각 노드가 연결된 edge들을 대상으로 계산한다.

위와 같은 특징 때문에 성능은 상대적으로 낮지만 음수 가중치를 포함하는 그래프에도 적용이 가능하다.

관련 문제